Méthode du calcul de structure par éléments finis

Les trois étapes du calcul par éléments finis

1- Le Pré-traitement

Définition des matériaux
Définition des conditions aux limites
Définition du type de calcul
Réalisation du maillage (discrétisation en éléments finis)

 

 2- Le Calcul numérique

Résolution numérique de la méthode des éléments finis
Mode implicite (indépendant du temps)
Mode explicite (dépendant du temps)
Obtention des déformations
Obtention des contraintes
Obtention des modes propres de vibration
Obtention des réponses temporelles dans le cas du calcul crash

 

3- Le Post-traitement

Exploitation des déformations
Exploitation des contraintes
Exploitation des modes propres
Exploitation des signaux temporels en mode explicite
Réalisation de préconisations de tenues statique, dynamique, fatigue
Préconisation d'améliorations le cas échéant
Réalisation du rapport de calcul ou note de calcul

 

La démarche numérique du calcul par éléments finis

1- Détermination des matrices de rigidités de chaque élément (1 élément = 1 maille)

[Kij]

2- Assemblage

Obtention de la matrice de rigidité globale [K]

3- Introduction des conditions aux limites

=> obtention d'un système d'équations linéaires :
[K] . {U} = {F}

{U} = déplacement
{F} = chargement en effort

4- Résolution de : {U} = [K]^-1 . {F}

=> obtention des déplacements {U}
=> puis obtention des contraintes et réactions aux conditions aux limites

 

Contraintes principales

Le tenseur des contraintes caractérise les efforts intérieurs définis pour chaque volume unitaire de matière. Il permet de décrire précisément l’état de contrainte en chaque point et est noté :

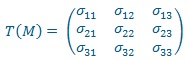
Sachant que les termes hors diagonale correspondent à du cisaillement, et appartenant souvent à la base vectorielle (X, Y, Z), il peut aussi s’écrire :

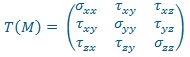
Les contraintes peuvent être exprimées dans une base telle que le tenseur des contraintes est une matrice diagonale : on parle de contraintes principales :

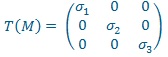
Les contraintes principales permettent d'interpréter immédiatement le(s) type(s) de sollicitations subi(s) par la matière, traction, compression, cisaillement, à la différence des critères de Von Mises et Tresca comme présenté ci-après.

Post-traitement : Critères de Plasticité de Von Mises et Tresca

Von Mises

Le critère de plasticité permet de se positionner par rapport à la Re :

• contraintes ≤ Re : non-plastification, d'où existence d'un potentiel de tenue en fatigue
• Contraintes > Re : plastification, potentiel de tenue en fatigue réduit, voire inexistant

Le critère de von Mises est le plus couramment utilisé.

Critère de von Mises :

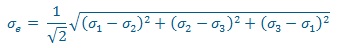
ou

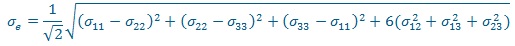
Tresca

 

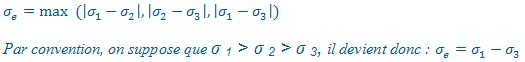
Ces critères prennent en compte les composantes de contraintes en traction, compression, cisaillement pour donner un niveau de contrainte isotrope (le même dans toutes les directions).
Ces critères indiquant un niveau de contrainte isotrope, notre travail va donc consister en la traduction des ces contraintes pour déterminer les sollicitations types traction, compression, cisaillement, torsion, flexion, c'est le but du post-traitement...

 

La représentation graphique ci-dessous de ces deux critères permet de les comparer facilement.

Ellipse de Von Mises
Polygone de Tresca 

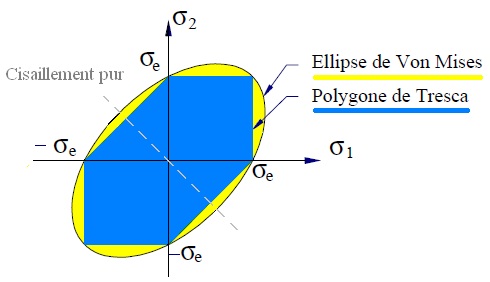
C’est en cisaillement pur que la différence entre les critères de Tresca et Von Mises est maximale.
En cisaillement pur, Von Mises prévoit une rupture à 0.577xRe alors que Tresca à 0.5xRe.
Tresca étant plus conservatif (la limite de contrainte admissible est ≤ à Von Mises), il est préférable de l’utiliser en cisaillement pur.
Nous rappelons que ces deux critères sont valables seulement pour les matériaux isotropes.

Bien entendu, nous déterminons intuitivement le type de sollicitation subi par la structure, notamment traction,  compression, flexion, torsion.
Mais pour le cisaillement, c'est plus délicat et beaucoup moins intuitif. En effet, même si les critères de Von Mises et Tresca prennent en compte le cisaillement, le faire apparaître en post-traitement demande une petite manipulation.
Le cisaillement est une combinaison de contraintes en traction et compression de valeurs absolues équivalentes sur une section matière. Et donc, pour caractériser une zone soumise à cisaillement, il faut extraire les contraintes principales  issues du tenseur des contraintes diagonalisé (le tenseur) sur une section matière carrée et vérifier qu'une diagonale de ce carré est soumise à de la traction et que l'autre diagonale est soumise à de la compression avec des valeurs abolues équivalentes.